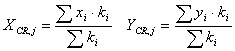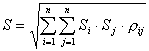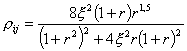ÍNDICE

• Introducción
• Para qué puede servir el listado
• Ejemplo
  • Datos para la realización del ejemplo
  • Determinación del centro de masas y viabilidad de losa de cimentación
  • Determinación del punto de paso de las resultantes bajo acciones del viento
  • Determinación cortante total debido a sismo, por planta y en la base

Introducción

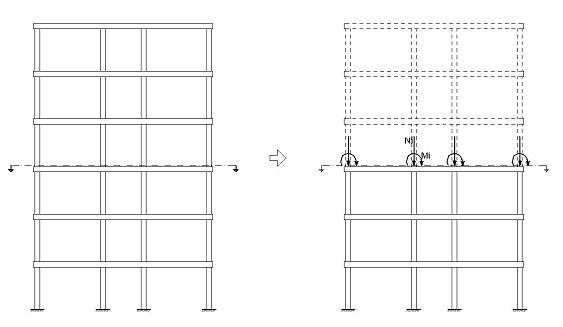
A partir de la versión 2010.e aparece en CYPECAD un nuevo tipo de listado de esfuerzos de pilares, pantallas y muros. En el programa se puede ver como “Sumatorio de esfuerzos de pilares, pantallas, y muros por hipótesis y planta”.

En el listado sólo se mostrarán esfuerzos de pilares, pantallas o muros, por tanto, cualquier elemento en el que apoye la totalidad o parte de una estructura, que no sea uno de los anteriores, no se mostrará en el listado. Por supuesto, si otro elemento provoca esfuerzos en un pilar, estos quedaran reflejados en el listado, ya que vienen del cálculo de la estructura, pero si hay otros elementos que van a cimentación además de los pilares (como por ejemplo viga con vinculación exterior) el sumatorio de cargas a la planta de cimentación real será superior al que se muestra en el listado.

Al nivel de la planta i, en el listado se muestran los esfuerzos en cada pilar, (suponiendo un corte de la estructura justo por encima de la cara superior del forjado, como se muestra en la imagen anterior), referidos a su propio eje, y referidos al origen de coordenadas. Además, se muestra la suma de esfuerzos de todos los pilares referidos al origen de coordenadas del plano horizontal situado a la cota correspondiente.

Para qué puede servir el listado

Con este listado se conocen las cargas actuantes, por encima de la cota de la base de los soportes sobre una planta, tanto a nivel de pilar, como a nivel global, por tanto, es posible utilizarlo con varias finalidades.

Es posible con unos cálculos sencillos conocer el centro de masas y el peso total del edificio, utilizando los datos del listado proporcionados bajo la hipótesis de cargas permanentes.

Podemos hacer una estimación de la viabilidad de una losa de cimentación, estudiando la tensión media de trabajo bajo la misma.

En alguna ocasión será interesante conocer la intersección de la línea de paso de la resultante con el plano de cimentación, bajo la acción del viento por ejemplo.

Podemos conocer el cortante total de cada planta y el cortante en la base del edificio debido al sismo, además este dato es necesario en algunas normativas sismorresistentes.

Se realizan a continuación algunos ejemplos de las posibilidades mencionadas, partiendo de la obra del ejemplo de cálculo del manual.

Ejemplo

Para la realización de los ejemplos se parte del ejemplo de cálculo del manual, obra a la que pueden acceder los usuarios del programa, en “Gestión de archivos”. Para ello deben pinchar en el botón “Ejemplos”, y abrir la obra “Manual”, que tiene por descripción “Ejemplo práctico de cálculo”.

Datos para la realización del ejemplo

El ejemplo se ha realizado con las siguientes acciones

Se han introducido cargas de viento según CTE-DB AE, con zona eólica B, grado de aspereza IV (zona urbana), y haciendo la simplificación (ya que queda del lado de la seguridad) de asignar anchos de banda de 10 m, tanto en X como en Y en todas las plantas, resultando los siguientes valores de cargas por planta:

Se ha introducido sismo según NCSE-02,  con las siguientes características:

• No se realiza análisis de los efectos de 2º orden
• Acción sísmica según X
• Acción sísmica según Y
• Clasificación de la construcción: Construcciones de importancia normal
• Aceleración sísmica básica (ab): 0.140 g
• Coeficiente de contribución (K): 1.00
• Coeficiente adimensional de riesgo (r): 1
• Coeficiente según el tipo de terreno (C): 1.30 (Tipo II)
• Coeficiente de amplificación del terreno (S): 1.035
• Amortiguamiento: 5% (respecto del amortiguamiento crítico)
• Fracción de la sobrecarga a considerar: 0.50
• Número de modos: 6
• Coeficiente de comportamiento por ductilidad: 2 (Ductilidad baja)
• Aceleración sísmica de cálculo (ac): 0.145 g

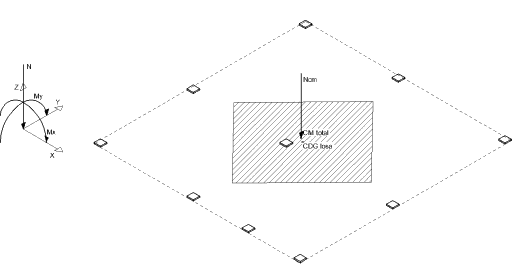
Determinación del centro de masas y viabilidad de losa de cimentación

Para la determinación del centro de masas, utilizaremos los datos del listado, a nivel de cimentación, para la hipótesis de cargas permanentes, y referidos al origen de coordenadas. Los valores proporcionados por el programa son los siguientes:

Para la determinación del centro de masas, utilizaremos lógicamente:

Se tiene como resultado:

Se puede observar que la resultante debida a cargas permanentes cae dentro del núcleo central de la superficie ocupada por el edificio en el plano de cimentación.

Para el estudio de la viabilidad de una losa, bastará con obtener la tensión media bajo cargas verticales. Así que a las cargas permanentes habrá que añadir la sobrecarga de uso, y el peso de la losa.

Los valores de esfuerzos proporcionados por el programa para la hipótesis de sobrecarga de uso, sumados y referidos al origen son los siguientes:

Y el peso de la losa, suponiéndola de 60 cm de canto es:

Para la estimación de la tensión media utilizamos:

Se obtienen entonces los valores de tensión media

Este resultado es válido siempre que las líneas de acción de las tres fuerzas verticales, pasen por el núcleo central, algo que se puede fácilmente verificar a simple vista.

De esta manera podemos comparar con la tensión proporcionada en el informe geotécnico si va a ser posible una solución mediante zapatas; si fuese más del doble, por ejemplo 2 Kp/cm², quiere decir que ocuparemos con las zapatas previsiblemente menos del 50% de la superficie, valor frontera para tomar la decisión entre zapatas y losa.

Si la tensión fuera del orden de 1 Kp/cm² sería una solución adecuada la losa coincidente con el perímetro de los pilares, pues la transmitida ronda los 0.71 Kp/cm², inferior a la admisible.

Caso de que la tensión fuera inferior a 0.715, por ejemplo 0.5 Kp/cm², necesitaríamos aumentar la superficie hasta llegar a la proporción de tensiones:

Determinación del punto de paso de las resultantes bajo acciones del viento

Que haciendo de forma aproxima la raíz, sería un cuadrado de lado 11.7 m, y teniendo en cuenta que nuestra losa tiene un lado medio de 9.70 m, bastaría con aumentar un metro de vuelo a cada lado, quedando la losa, para poder encajarla a 0.50 Kp/cm², de:

Y si fuera todavía inferior a este valor, aunque en la losa de cimentación indicada se podrían seguir aumentando vuelos y canto para aumentar superficie de reparto y mayor rigidez, sería posible tomar la decisión de tantear cimentaciones profundas para este caso, decisión obligatoria si no fuera posible dar vuelos a la losa.

Determinación cortante total debido a sismo, por planta y en la base

A continuación, se muestran los datos del sumatorio de fuerzas de viento a la cota de cimentación, y referidas a origen. Sólo miraremos el viento en el sentido positivo de cada una de las dos direcciones principales.

Se vuelven a mostrar los datos del sumatorio de esfuerzos, referidos a origen, de las hipótesis de cargas permanentes y de sobrecarga de uso.

Para la determinación del punto de paso de la resultante realizamos las combinaciones con las hipótesis de carga permanente y sobrecarga, cada combinación dará un punto de paso.

Actuando de la misma forma que en el primer ejemplo, obtenemos las coordenadas de los puntos de paso.

Los puntos de paso son los siguientes:

Además un cálculo rápido permite calcular los centros de rigidez de las plantas, para poder evaluar la torsión debida a acciones horizontales:

donde la letra i representa un pilar, y la letra j la planta.

Los centros de rigidez son:

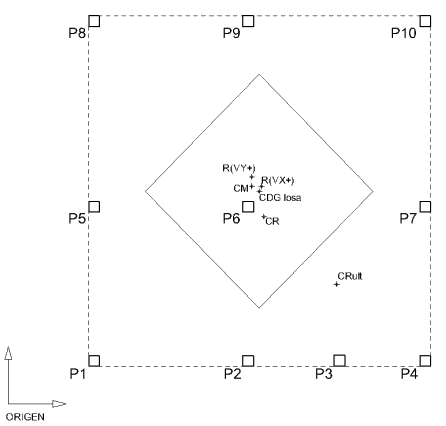
Para una mejor visualización de los resultados, éstos se muestran en la siguiente figura:

Como se puede observar, las líneas de paso de las resultantes de viento (sólo hemos obtenido los vientos positivos en X y en Y), pasan por el núcleo central de la figura formada por el contorno de los pilares.

El listado de sumatorio de esfuerzos, en caso de sismo, nos proporciona la información de los esfuerzos debidos a los modos de vibración, por tanto, para obtener los totales debemos realizar la superposición modal. CYPECAD realiza la superposición modal por el método de la Combinación Cuadrática Completa, que tiene en cuenta el posible acoplamiento modal.

Sea S la variable cuyo valor máximo queremos obtener y S_i, su valor en el modo i, el valor S por el método de la Combinación Cuadrática Completa es:

Siendo:

Donde r es la relación entre las frecuencias i, y  j, y  ξ es el coeficiente de amortiguamiento.

No obstante, para un cálculo más rápido se podrá utilizar el método de la Raíz Cuadrada de la Suma de los Cuadrados, que es el siguiente:

Sea S la variable cuyo valor máximo queremos obtener y Si, su valor en el modo i, el valor S por el método de la Raíz Cuadrada de la Suma de los Cuadrados es:

Este método se considera una aproximación válida siempre que dos períodos consecutivos cualesquiera de una estructura difieran en más de un 10%, debido al posible acoplamiento modal que podría llevarnos a sobrevalorar o infravalorar el resultado.

Para este caso, las diferencias entre los períodos de los diferentes modos de vibración es, en algunos casos, menor que el 10 %. A continuación, se muestran los períodos de los diferentes modos, obtenidos del listado de coeficientes de participación.

Obtendremos los resultados de los dos métodos a continuación.

Método Raíz Cuadrada de la suma de los Cuadrados (RCSC)

Por el método de la Raíz Cuadrada de la Suma de los Cuadrados, a partir del listado de sumatorio de esfuerzos, se obtienen los siguientes resultados, referidos a origen.

Por tanto, los cortantes basales son:

A continuación obtendremos el centro de masas de cada planta, tomando los valores del listado de sumatorios, pero con la particularidad de tomar para ello el 100 % de las cargas permanentes y el 50% de la sobrecarga de uso, ya que parece lo más lógico al haber creado los modos de vibración a partir de esta premisa. Con las relación entre momento y axil ya mencionada se obtendrán los resultados.

Como conocemos el centro de masas de cada planta podemos trasladar el cortante de cada planta y la torsión de la misma, desde el centro de gravedad.

Método de la Combinación Cuadrática Completa (CQC)

Por el método de la Combinación Cuadrática Completa, a partir del listado de sumatorio de esfuerzos, y con ayuda de una hoja de cálculo, para este ejemplo se ha obtenido la composición modal resultando, referidos a origen, los siguientes valores de los que se deducen directamente el cortante total por planta y en la base del edificio.

Por tanto, los cortantes basales son:

Como conocemos el centro de masas de cada planta (calculado anteriormente) podemos trasladar el cortante de cada planta y la torsión de la misma desde el origen de coordenadas al centro de masas de la misma.

Conclusión comparativa de los dos métodos

Como se puede observar los resultados del método de la Raíz Cuadrada de la Suma de los Cuadrados no están tan alejados de los del método de la Combinación Cuadrática Completa.

No obstante, es cierto que cuanto más cercanos estén los períodos de los modos que más masa movilizan, más error cometeremos con el método de la Raíz Cuadrada de la Suma de los Cuadrados, aunque ofrece una buena aproximación. Por otro lado, si los modos están más próximos, el método de la Combinación Cuadrática Completa proporciona mejores resultados.

Para este ejemplo, entre el primer y segundo modo hay una diferencia aproximadamente del 9% y, entre el segundo y el tercero, un 25 %.