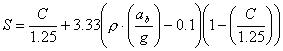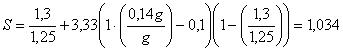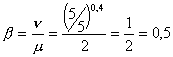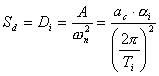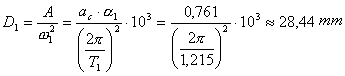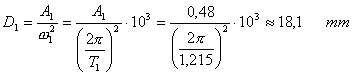A continuación se muestran dos ejemplos de listados de coeficientes de participación

ÍNDICE

1^er ejemplo

Introducción

Primero realizaremos un ejemplo para la determinación de la aceleración de cálculo, incluida la ductilidad, según el modo de vibración, y el coeficiente del modo, ya que se trata de cálculos sencillos.

Datos para el ejemplo

Partiremos de la obra del ejemplo de cálculo del manual, obra a la que pueden acceder los usuarios del programa. Para ello se pincha en el botón “Ejemplos”, en “Gestión de archivos”, y se abre la obra “Manual”, que tiene por descripción “Ejemplo práctico de cálculo”.

Introducimos sismo según NCSE–02, con las siguientes características.

• No se realiza análisis de los efectos de 2º orden
• Acción sísmica según X
• Acción sísmica según Y
• Clasificación de la construcción: Construcciones de importancia normal
• Aceleración sísmica básica (a_b): 0.140 g
• Coeficiente de contribución (K): 1.00
• Coeficiente adimensional de riesgo (r): 1
• Coeficiente según el tipo de terreno (C): 1.30 (Tipo II)
• Coeficiente de amplificación del terreno (S): 1.035
• Amortiguamiento: 5% (respecto del amortiguamiento crítico)
• Fracción de la sobrecarga a considerar: 0.50
• Número de modos: 6
• Coeficiente de comportamiento por ductilidad: 2 (Ductilidad baja)

Listado proporcionado por el programa

Veamos los datos proporcionados por el programa en el listado de coeficientes de participación.

En el listado, T es el período de vibración del modo en segundos.

Lx, Ly, y Lgz, son coeficientes de participación normalizados de cada modo, y en cada dirección del análisis. Se podría decir que son las componentes de un vector unitario, en el que se describe la cantidad de desplazamiento en x del modo (Lx), la cantidad de desplazamiento en y del modo (Ly), y la cantidad de giro (Lxy).

Mx, y My es la masa movilizada del modo. Recordemos que la norma NCSE-02, nos indica que se ha de superar el 90% de masa movilizada.

R, es la relación entre la aceleración de cálculo con la ductilidad asignada a la estructura, y la aceleración obtenida sin ductilidad.

A, es la aceleración de cálculo, incluyendo la ductilidad.

D, es el coeficiente de modo, equivale al desplazamiento máximo del grado de libertad dinámico.

Obtención de los valores A, D y R

Según la norma, la aceleración de cálculo se calcula de la siguiente manera.

Para los dados:

Sustituyendo se obtiene:

Para el ejemplo anterior:

Calculamos el espectro también según norma:

Si 

Si

Si

En nuestro caso:

luego:

Si

Si

Si

El período del modo 1 es 1,215 con lo que;

El coeficiente de respuesta es:

donde  es el factor de amortiguamiento, y es función del amortiguamiento , y  es la ductilidad.

En nuestro ejemplo:

Aplicando el coeficiente de respuesta obtenemos el valor a aplicar al modo 1.

Si multiplicamos este valor por la aceleración de cálculo:

Haríamos la misma operación para cada uno de los modos.

Lo que el programa lista como aceleración de cálculo A_i, incluyendo la ductilidad, es el valor de , para cada modo.

El valor de R es relación entre la aceleración de cálculo usando la ductilidad asignada a la estructura y la aceleración de cálculo obtenida sin ella, que lógicamente, con nuestra norma, coincide con la propia ductilidad.

El valor D es el desplazamiento máximo asociado al modo, se deduce a partir de:

Despejamos:

El programa muestra el desplazamiento en milímetros, para nuestro ejemplo obtendríamos:

Este desplazamiento no tiene mucho significado físico, ya que se refiere a un único modo y el programa realiza una superposición de todos los modos, con lo que no sería válido, por ejemplo, para el dimensionado de juntas.

Masa total desplazada

El programa muestra al final del listado de coeficientes de participación una pequeña tabla, en la que se muestra la totalidad de la masa desplazada, tanto en una dirección como en la otra.

En el ejemplo que nos ocupa se muestra la suma de las masas movilizadas en cada modo, y según norma NCSE–02 se ha de movilizar más del 90% de la masa, en el caso de no llegar al 90%, tendremos que aumentar el número de modos a analizar hasta sobrepasar dicho valor, evidentemente sin superar el máximo de modos que es posible analizar para el edificio, que es para el caso normal de edificio en un único bloque continuo, de tres modos de vibración por planta, tantos como grados de libertad dinámicos posee nuestra estructura.

2º ejemplo

Con sismo según análisis modal espectral

Ahora vamos a realizar otro ejemplo, utilizando el “análisis modal espectral”,  con los siguientes datos:

• No se realiza análisis de los efectos de 2º orden
• Acción sísmica según X
• Acción sísmica según Y
• Aceleración (fracción de g) a_c: 0.14
• Fracción de la sobrecarga a considerar: 0.50
• Número de modos: 6
• Ductilidad µ= 2

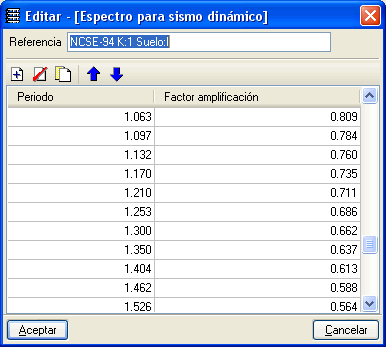
Hemos seleccionado un espectro de la biblioteca, en particular, el denominado “NCSE – 94 K:1 Suelo I”, importándolo inicialmente, y cuyo factor de amplificación α(T) podemos ver en ordenadas y período T, en segundos, en abscisas. Al editar la tabla se observan los valores:

Con estos valores calculamos la estructura y obtenemos el listado de coeficientes de participación que, como es evidente, tendrá las mismas características de modos de vibración que en el ejemplo anterior, ya que estos dependen de la estructura propia y no de la acción sísmica que se le aplique, los valores de R, A y D serán distintos, ya que sí dependen de la acción sísmica aplicada.

Listado proporcionado por el programa

Veamos los datos proporcionados por el programa en el listado de coeficientes de participación.

Con los significados ya mencionados en el anterior ejemplo.

Obtención de los valores A, D y R

R, es la ductilidad que en análisis modal espectral se introduce como dato, por tanto:

R = 2

La aceleración de cálculo, a_c, (que no la básica), englobando todos los coeficientes de importancia de la construcción, tipo de construcción, amortiguamiento, etc. La hemos definido en la introducción de datos como:

a_c = 0.14 g

De la tabla y para el primer modo, el valor del factor de amplificación, la ordenada del espectro para el período del primer modo es:

Y el valor de la aceleración será por tanto:

Y el valor del desplazamiento: